随着5G产品的大规模商用，产品遍布全球高原、沙漠、沿海等地区，面临着各种复杂的使用工况，产品的可靠性寿命受到更严苛的考验。针对市场产品需达到一个预期寿命比如10年或20年。当然这个不太可能将产品放在实际工况下做这么长时间的实验，当前主要是通过加速实验判断预期寿命。

加速实验中，获取温循寿命主要通过的是高低温加速实验，这种实验一方面成本较高，并且只能暴露问题，无法提出解决方案，比如实验完成后知道器件焊点温循寿命低，在设计端怎么做可提高温循寿命呢。通过有限元仿真可较好避免上述两个弊端。

本文通过ABAQUS有限元仿真软件，模拟分析典型QFN器件的焊点在热循环下的可靠性寿命，通过实验对比判断仿真的精度，并且研究影响QFN焊点温循寿命的相关因子。

器件焊点温循失效机理

由于PCB与器件的热膨胀系数（CTE）不匹配，在长期高低温过程中形成交变载荷，导致焊点裂纹的萌生及扩展，最终导致焊点的失效。这种失效模式属于低周疲劳失效。

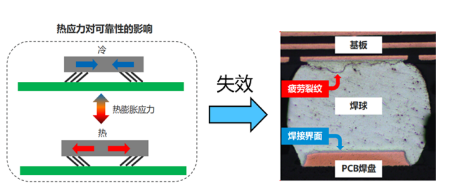
图1 器件焊点温循失效机理

当前业界对焊点这种失效形式的预测模型有以下几类:

基于应变损伤的Coffin-Manson方程和其修正方程

基于损伤能量，典型的模型为Darveaux方程

基于蠕变变形的预测模型

基于断裂参量为基础的预测模型

几类模型都可以预测温循寿，最为常用的是基于应变损伤的Coffin-Manson方程和基于损伤能力的Darveaux方程，而其中C-M方程常用于QFN类焊点温循寿命预测，Darveaux常用于BGA等新式封装的寿命预测。

仿真参数选择及模型建立

因素分析

本文主要由两部分内容组成：实测焊点温循寿命和仿真对比；研究影响QFN焊点温循寿命的相关因子。

实际进行温循寿命实验的器件重点参数信息为：封装尺寸6*6mm，PCB厚度2.4mm，PCB CTE16，焊点高度0.1mm，散热焊盘面积占比为0.5。

首先，建立三维有限元模型分析焊点在温循循环过程中的应力应变，其中采用Anand粘塑性本构模型描述无铅钎料SAC305的力学行为，采用修正后的Coffin-Manson寿命预测模型计算初始设计情况下的QFN封装焊点温循寿命，并和温循实验进行对比，判断仿真精度。

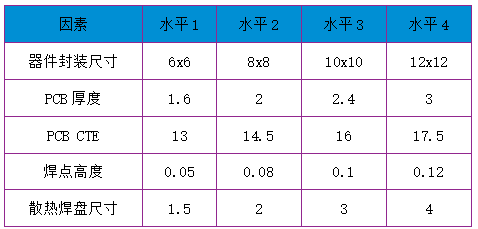
表1 正交分析因子及水平表

在此芯片相关尺寸基础上对上述5个因子进行研究，采用Taguchi实验设计(Design of experiment，DOE)方法建立L16（45）正交实验表进行最优因子组合设计，最后采用有限元分析方法对最优因子组合设计结果进行验证，得到最优因子组合设计情况下的热疲劳寿命。

有限元模型

由于几何结构的对称性，采用ABAQUS和Hypermesh等有限元仿真软件建立三维1/4有限元模型，其中包括QFN封装、PCB和焊点。模型采用六面体单元进行网格划分，单元类型为C3D8I，焊点为Anand粘塑性材料本构，其他材料均为线弹性材料本构。

a、整体有限元仿真模型

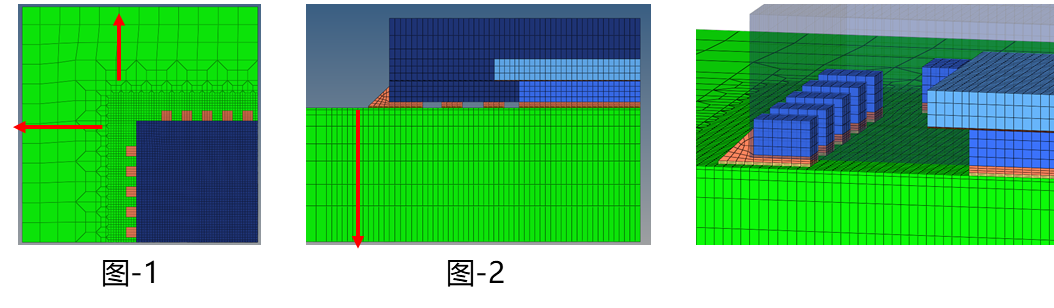
（b）局部有限元仿真模型

图2仿真分析的有限元模型

温循寿命求解

焊点在温循循环载荷下的等效应力和等效塑性应变是影响热疲劳可靠性的重要因素，在高温驻留阶段的影响尤为明显。温循循环完成后，提取焊点在最后一个温度循环中高温驻留阶段结束时的等效应力和等效塑性应变分布进行分析，确定最易发生热疲劳失效的焊点和位置，即关键焊点和关键位置

结合图3和图4研究可发现。最大等效应力和最大等效塑性应变均位于同一位置，即器件的边角处焊点与引脚结合界面的端部，说明在温度循环载荷下，疲劳裂纹极易在关键焊点与引脚结合界面端处萌生。从图3图4和图5来看，实测的失效位置及裂纹形态均与仿真比较符合。

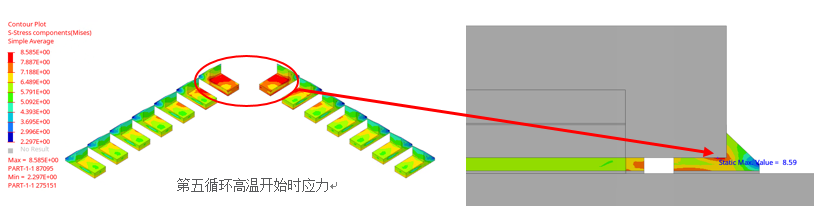
图3焊点的等效应力分布云图(Mpa)

图4焊点的等效塑性应变分布云图 图5失效边角焊点的切片图

通过图3和图4确定关键焊点和关键位置后，提取关位置的等效应力、等效塑性应变随温度循环载荷的变化进行分析，分别如图6、图7所示：

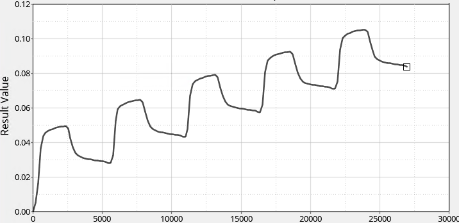
图6焊点等效应力随时间变化

图7焊点等效应力随时间变化

从图6、图7可以发现，在5Cycle循环中，应力逐渐趋于稳定。应变的增加量也趋于稳定。我们采用Engelmaier Wild修正的Coffin-Manson方程通过提取焊点的等效塑性应变进行温循寿命计算，计算公式为：

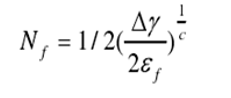
式中：Nf—热疲劳平均寿命；△γ—等效非弹性剪切应变范围；△ɛ—等效非弹性总应变范围；ɛf—疲劳韧性系数=0.325；f—循环频率。此处c与热循环的温度和频率有关。

C=-0.442-6*10-4Tm+1.74*10-2ln(1+f)、Tm=(Tmax+Tmin)/2，式中：Tm—热循环的平均温度，Tmax—循环最大温度值，Tmin—循环最小温度值。

根据以上公式求得进行温循实验的QFN器件的温循仿真寿命为560Cycle，而实际实验的测试值为500Cycle，温循仿真和实测的吻合度为89.3%。

数据分析

通过上节内容我们获取了仿真吻合度，本节内容研究影响焊点温循寿命的相关因子，将16组正交实验的结果进行提取，并进行主效应分析，从图8可发现，在其他因子固定的情况下，器件的封装尺寸、PCB厚度、PCBCTE数值和焊点的寿命成负相关；焊点高度和焊点的疲劳寿命成正相关；散热焊盘面积占比疲劳寿命影响较小；

图8焊点疲劳寿命主效应分析示意图

获取主效应影响后仅知道了各因子对温循寿命的影响是正相关或负相关，工程师需要知道哪些因子对疲劳寿命的影响最大，我们接下来进行显著性因子分析：

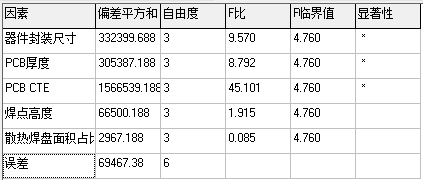
图9-1显著性分析表

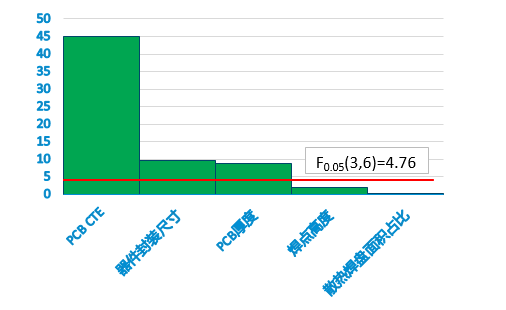
图9-2显著性分析表

通过图9-1和9-2可得出，器件封装尺寸、PCB厚度、PCB CTE均为显著性因子，但PCB CTE的显著性远远其他几项，故在设计时为了保证焊点的温循可靠性寿命应着重考虑PCB的CTE。

将原始器件尺寸按主效应和显著性分析进行优化，得到数据如图10所示，通过优化使焊点的温循寿命有较大提升。

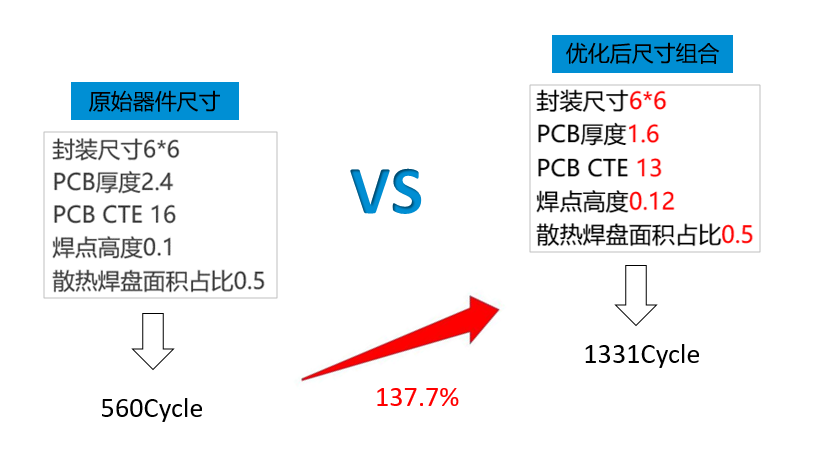
图10优化效果提升图

总结

高低温加速实验成本高、周期长，无法提出优化方案。仿真可以较好的解决上述问题。当前焊点温循仿真在部分QFN器件的寿命预测上能达到85%以上的精度，仿真得到LOW-CTE板材对焊点温循寿命有显著影响在实际项目中得到验证。

（文章来源：actSMTC）