文氏电桥振荡电路(Wien bridge oscillator circuit)，简称“文氏电桥”，是一种适于产生正弦波信号的振荡电路之一，此电路振荡稳定且输出波形良好，在较宽的频率范围内也能够容易调节，因此应用场合较为广泛。

如下图所示为基本文氏电桥振荡电路：

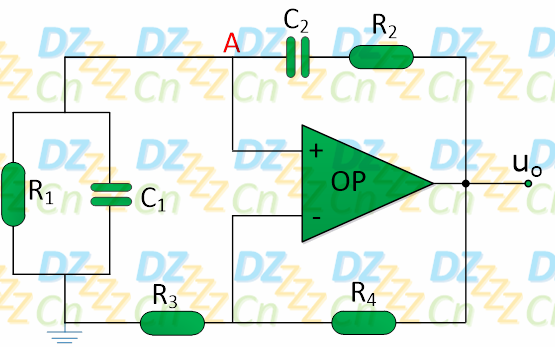
其中，R1、R2、C1、C2组成的RC串并网络将输出正反馈至同相输入端，R3、R4则将输出负反馈至运放的反相输入端，电路的行为取决于正负反馈那一边占优势(为便于分析，通常都假设R1=R2=R且C1=C2=C，当然这并不是必须的)。

可以将该电路看作对A点输入(即同相端电压)的同相放大器，因此该电路的放大倍数如下：

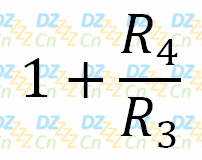
可以证明，当放大倍数小于3时(即R4/R3=2)，负反馈支路占优势，电路不起振;当放大倍数大于3时，正反馈支路占优势，电路开始起振并不是稳定的，振荡会不断增大，最终将导致运放饱和，输出的波形是削波失真的正弦波。

只有当放大倍数恰好为3时，正负反馈处于平衡，振荡电路会持续稳定的工作，此时输出波形的频率公式如下所示：

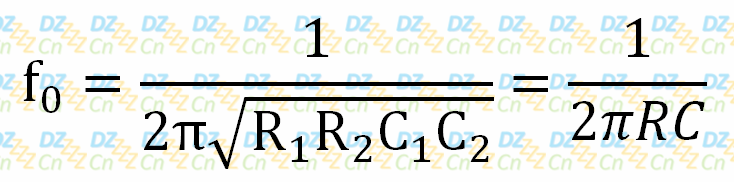
也可以这样理解：电路刚上电时会包含频率丰富的扰动成分，这些扰动频率都将会被放大，随后再缩小，依此循环，只有扰动成分的频率等于f0时，放大的倍数为3，而缩小的倍数也为3，电路将一直不停地振荡下去，也就是说，频率为f0的成分既不会因衰减而最终消失，也不会因一直不停放大而导致运放饱和而失真，相当于此时形成了一个平衡电桥。

但是这个电路的实际应用几乎没有，因为它对器件的要求非常高，即R4/R3必须等于2(也就是放大倍数必须为3)，只要有一点点的偏差，电路就不可能稳定地振荡下去，因为元件不可能十分精确，就算可以做到，受到温度、老化等因素，电路也可会出现停振(放大倍数小于3)或失真(放大倍数大于3)的情况。

我们用下图所示的电路参数进行仿真：

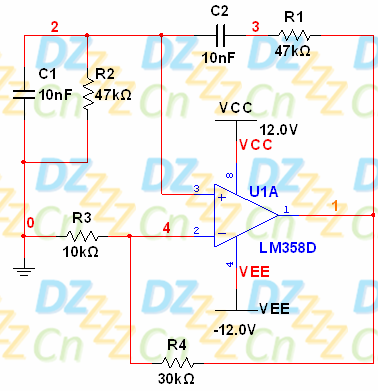
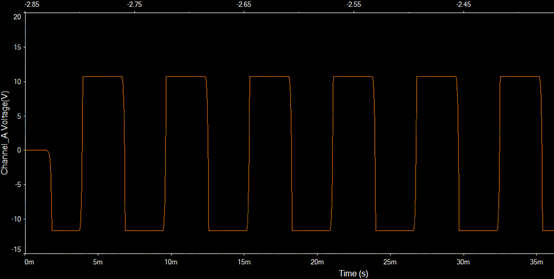
当R4=100K时，放大倍数为11，输出波形如下图：

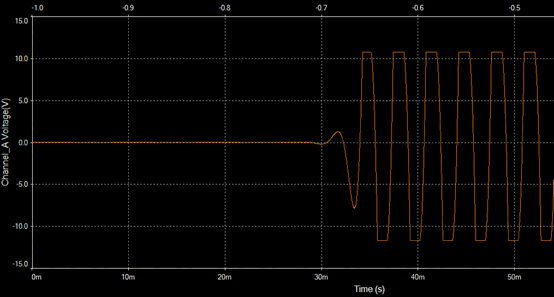
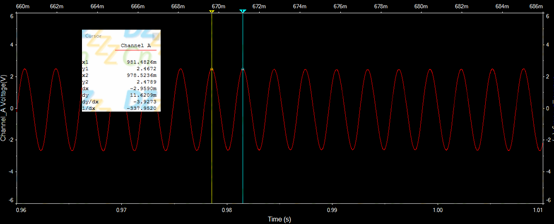
当R4=30K时，放大倍数为4，输出波形如下图：

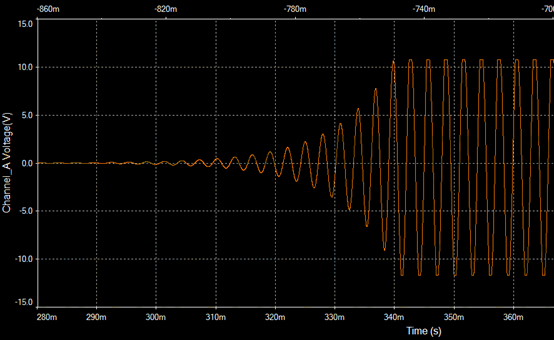
当R3=21K时，放大倍数为3.1倍，输出波形如下图所示：

当R3=20.1K时，放大倍数为3.01倍，输出波形如下图所示：

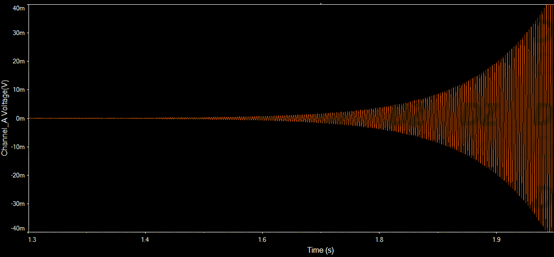
注意纵轴单位为mV(毫伏)，此时电路起振后不断地放大导致幅度增加(此图只是一部分)，但由于放大倍数太小，因此达到大信号电平需要更长的时间。

当R3=20K时，放大倍数为3倍，输出波形如下图所示：

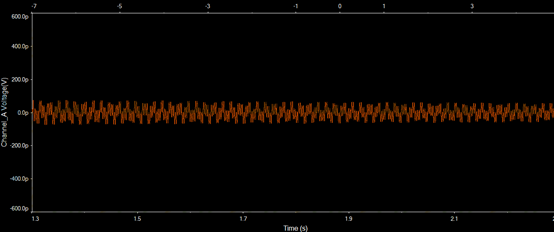
注意纵轴单位为pV(皮伏)，放大倍数太小，一直都处在小信号状态，什么时候达到大信号状态也无从得知，因此这里就没图了，不好意思。

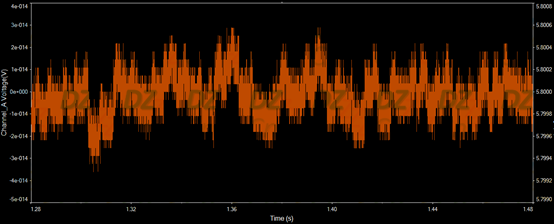
当R3=15K时，放大倍数为2.5倍(负反馈占优势)，如下图所示：

把局部放大后如下图所示，注意纵轴单位

可以看到，电路的放大倍数越大，则电路越容易起振，但只要放大倍数超过3，则输出波形都将出现削波失真，如果放大倍数设置恰好为3，则仿真时间要等很久才会有结果。实际用器件搭电路时，要做到放大倍数为3.00000XXXX可真不是件容易的事.

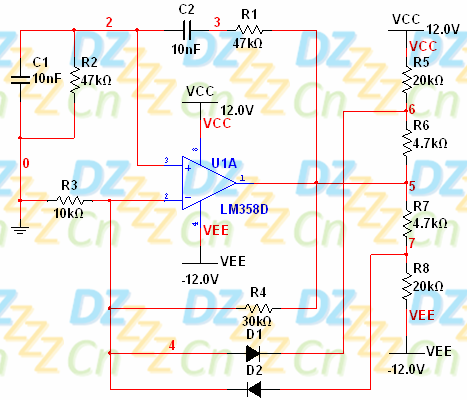
为了让电路更容易应用于实践，我们有必要对其进行优化，如下图所示：

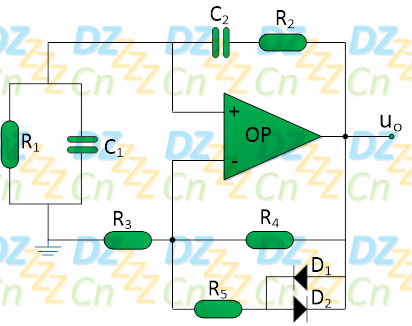
我们的修改思路是这样：当电路开始振荡时保证放大倍数大于3，这样可以使得电路容易起振，而当电路的振荡幅度增大到某个程度时，将其放大倍数自动切换为小于3，这样就能限制振荡的最大幅度，从而避免振荡波形出现削波失真。

这里增加了R5、D1、D2，当振荡信号比较小时，二极管没有导通，因此R5、D1、D2支路相当于没有，因此放大倍数大于3，而当振荡信号比较大时，二极管导通，相当于R5与R4并联，这样放大倍数就会小一些(合理设置R5的阻值，可以使其放大倍数小于3)。

我们用下图所示的电路参数进行仿真：

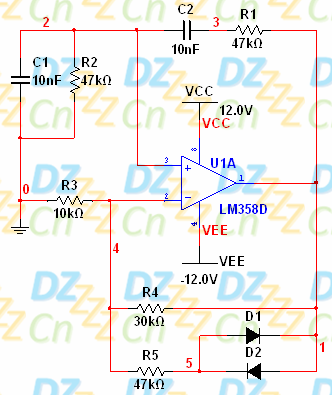
其输出波形如下图所示：

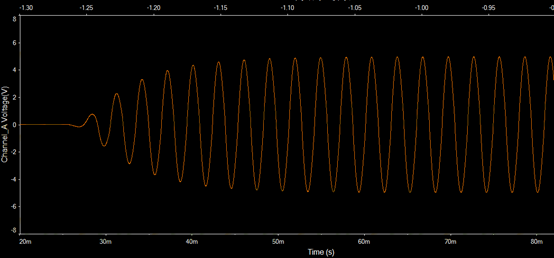
下图为局部放大的波形图，可以看到，此时的输出波形不再有失真。

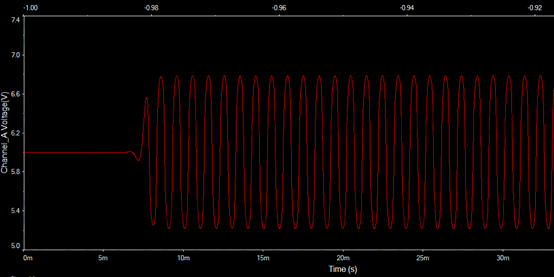
实际应用中，我们也可能需要单电源供电的振荡电路，如下图所示：

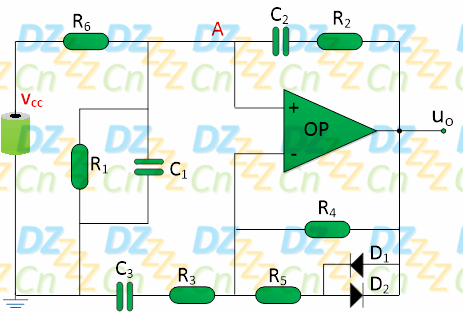
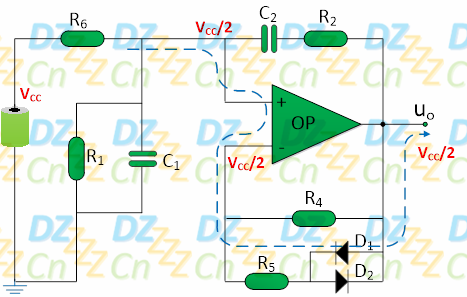
在单电源供电系统中，我们增加了电阻R6与电容C3，电阻R6的值通常与R1相同，这样两者对直流正电源VCC分压，则有A点的电位为(VCC/2)，再利用电容C3的“隔直流通交流”特性，使R4(R5)引入直流全负反馈，此时相当于一个电压跟随器，因此输出静态时输出电压为VCC/2，此时电路的直流通路等效如下图所示：

我们用下图所示的电路参数进行仿真：

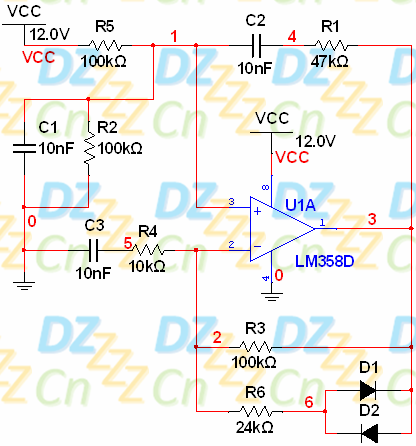
其输出波形如下图所示：

可以看到，输出正弦波是以6V(即12V的一半)作为中点的。

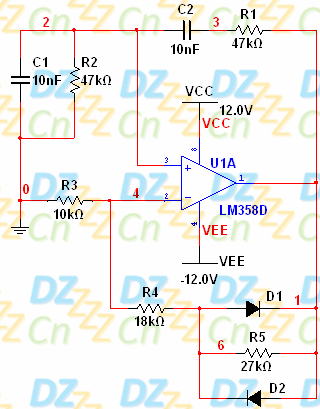
也有如下图所示相似的电路，读者可自行仿真，原理是一致的。

从原理上很容易看出，电路输出波形的幅度与二极管的正向压降有很大的关系，我们可以用下图所示电路来摆脱这个问题：

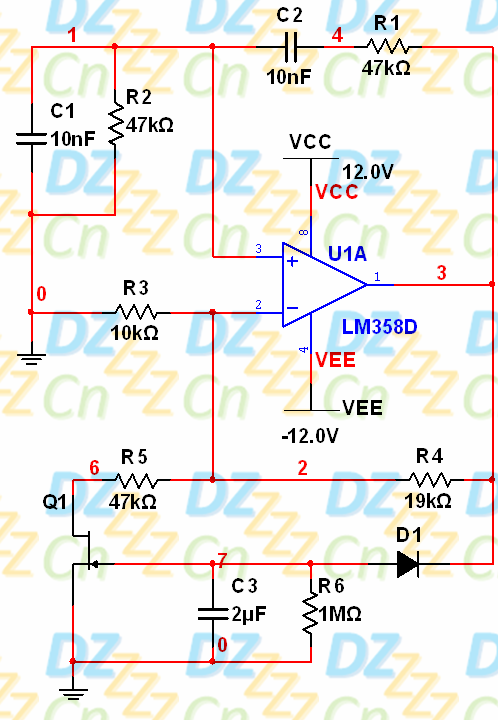
N沟道JFET的阀值电压VTH为负压，当VGS=0时(即电路刚上电时)，源-漏导通而将R5短接到地，R5与R3并联再与R4组成负反馈，此时电路的放大倍数约为3.3(大于3)，电路开始起振，振荡的幅度也会越来越大;当输出负压足以使VGS

下图也是一种稳幅电路，如下图所示，读者可自行分析：