智能制造是“中国制造2025”的主攻方向，是人工智能技术深度融入制造业的产物。越来越多的制造型企业，通过引入人工智能技术和智能化管理手段，逐步实现精益化管理以及企业资源最优化配置。生产调度是生产管理活动的指挥中心，伴随着数字化、网络化、信息化广泛而深入的普及和应用，智能化、精益化的生产调度， 也就是智能调度将会更合理地安排生产工序，缩短产品生产周期，成为企业增强核心竞争力的主要途径。智能调度指利用人工智能技术，依靠具备自主感知、自主决策、自主控制和自主学习能力的智能化设备，结合大数据、云计算和物联网技术，对人员、设备、任务、物料、工装和物流等进行动态调度，提出最佳的调度方案。

生产调度是一种组合优化问题，它没有有效的多项式时间算法，被证明是一种多项式复杂程度的非确定性问题（Non-deterministic Polynomial，NP）。1982 年， Kirkpatrick 等人将固体模拟退火思想引入组合优化领域， 提出一种用于解大规模组合优化问题的模拟退火算法。1992 年，Peter J.M 第一次提出采用模拟退火算法来求解作业车间调度问题，近年来不断涌现出各种改进算法用于解决车间调度问题。

传统模拟退火算法存在收敛速度慢和求解质量低等问题，很难直接将其嵌入现代化制造企业的生产过程执行系统（Manufacturing Execution System，MES），有必要优化设计一种高效的模拟退火算法，使其可以在运行MES 的硬件平台上，实时完成生产任务的智能调度。基于GPU 的异构系统成为现阶段高性能计算体系的一种主流设计方法，与同时期的中央处理器（Central Processing Unit， CPU）相比，GPU 具备高度并行、多线程等特点，其主要用途由图形渲染已经过渡到通用计算方面。

模拟退火算法

模拟退火算法来源于对固体退火过程的模拟，是一种基于概率的算法。在实际求解运算过程中，模拟退火算法从某个初始解和控制参数出发，求得给定控制参数值时相对最优解，然后减小控制参数t，对当前解重复持续“产生新解- 判断- 接受/ 舍弃”迭代过程，每经过这一过程就执行了一次蒙特卡罗（Monte-Carlo）算法。随着控制参数t 趋于零，算法终止最终求解得到组合优化问题的整体最优解。

模拟退火算法主要计算步骤：初始化参数，给定初始温度和终止温度；计算目标值增量；通过转移概率Pt 确定是否接受从当前解i 到新解j 的转移。

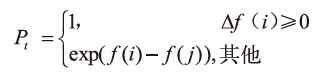
生产调度模型

生产调度工作要以生产计划为主线开展，通过监控感知设备实时掌握生产计划执行情况，能够及时快速地发现生产线出现的偏差，并采取有效地应对调度策略， 以减少生产过程等待时间。通过对企业资源及生产任务的合理配置和优化，保证生产过程顺利高效运行，发挥最大生产效率，创造更大企业价值。

在采用模拟退火算法解决生产调度问题之前，首先建立生产调度问题数学模型。本课题生产调度问题可抽象为一条生产线由m 台机器组成，经过多道工序加工n 个工件，且工序的顺序是不变的。调度算法为各工件分配在各机器上的加工时间，使某些性能达到最优。假设有n 项相互独立的任务T1，…，Tn，由m 台机械设备完成各项任务的m 道工序。

定义：M 为机器编码矩阵，mi，j 是任务Ti 的第j 道工序所用的机器编号，即。T 为工序时间矩阵，ti，j 为作业Ti 的第j 道工序所需时间，即ti，j ∈ T，其中。

本文从机器、时间以及工序等方面进行约束，并对生产调度问题做出以下假设：

1）按照特定工序加工，只有当一道工序结束之后方可进入下一道工序；

2）各工序时间可控，根据设计需求选择对应加工速度；

3）同一时刻，一台设备只能加工一个工件；

4）不可多台设备同时加工一个工件；

5）开始加工后不能中断，直至完成一个工件加工；

6）不考虑工件送往加工设备的运输时间。

生产调度的目标是通过优化各项任务在机器上的加工顺序，使得m 台机器上的n 项任务在完成时间尽量接近或等于最小值，即找对n 项任务的一个调度，使完成所有任务的时间f (n，m) 最短。

即求解

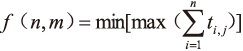
，其中j=1,2,…m。

面向智能调度的并行模拟退火算法

产品生产调度时，根据设备、人员、任务以及生产线情况，通过智能调度算法对每种产品进行生产排序， 为每一个子批选择合适的加工设备，同时确定该子批开始加工时间。通过对各加工设备和开始工作时间的最优调度，最终使得完成生产任务所需要的加工时间最短。

基于模拟退火算法的生产调度，从确定问题的目标函数开始，再将初始解代入目标函数，在控制降温系数递减过程中，重复进行“产生新解- 判断- 接受/ 舍弃” 的迭代过程，相当于执行了一次Monte-Carlo 算法过程， 随着控制参数趋于零时，得到最优智能调度方案，算法流程如图1 所示。

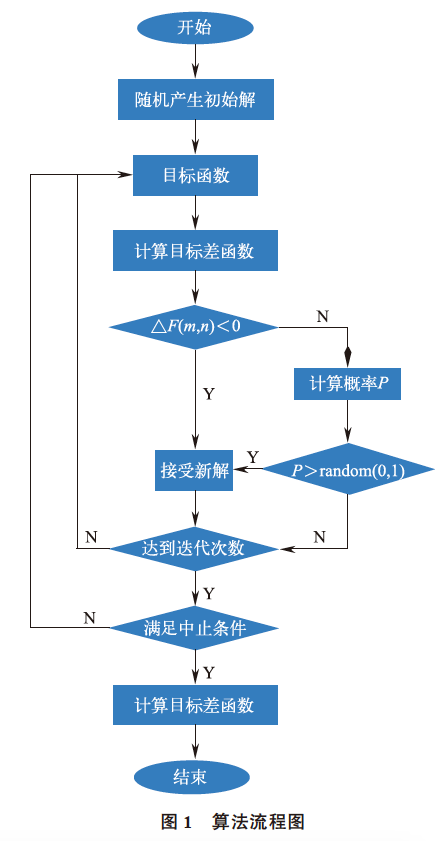
基于模拟退火算法的智能调度问题数学模型如下：

1）解空间。一次调度即是一个正数集， 其中1 ≤ iw ≤ n，1 ≤ w ≤ m×n，n 是任务数，m 是工序数。

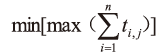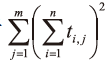2） 目标函数。调度问题是要使各机械设备完成n 项任务所用时间ti，j 之和最大值为最小， 即需求， 其中；j=1,2,…,m;，ti，j 可根据一次调度查表确定。易证其最小值对应于的最小值。

所以目标函数定义为

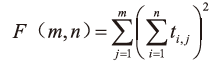
3）新解的产生。对完成任务先后顺序进行调整， 即集合中元素重新排列，形成新的调度，其中，n 是任务数， m 是工序数。

4）目标差函数。由目标函数可得，伴随于新解的目标函数差为

5）接受准则。

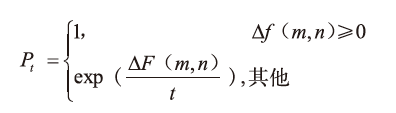
6）并行策略。本文建立的模拟退火算法并行计算模型分为任务级并行、数据级并行和线程级并行。采用两块图形存储器分别参与机器编码矩阵M 和工序时间矩阵T 的存储和运算。线程级并行是根据模拟退火算法的数学模型，结合图形处理器并行计算的硬件特点，将数值计算以及逻辑判断映射到图形处理器细粒度并发线程的具体实现过程。

仿真结果

本课题设计的智能调度算法能够适用于多品种机器零件的加工任务，目的是通过并行模拟退火算法求解得到最优调度方案。下面以铝合金薄壁耐压壳体加工过程为例，来验证算法的应用效果。铝合金薄壁耐压壳体加工一般需要经过配料、粗车、热处理、精车、铣床和钳床工艺流程，是6 道相互独立的工序。假定本课题有5 个不同规格的铝合金薄壁耐压壳体需要加工，生产线上有6 台工艺设备，不考虑各工序之间的等待时间。仿真时采用的硬件平台CPU 为Intel i5-8300，GPU 为Nvidia Tesla C2050，软件平台为Matlab2013，CUDA8.0。选取模拟退火初始温度为1 000℃，终止温度为0.001℃，循环迭代次数为2 000，降温系数为0.98，回火迭代系数为0.15，马尔科夫链长度为260。

定义机器编码矩阵M 和工序时间矩阵T：

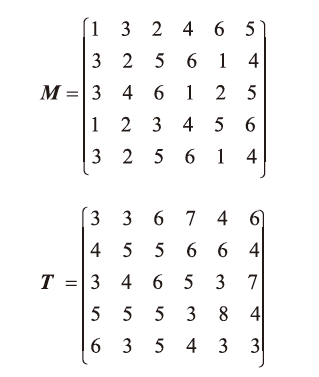
式中：矩阵T 的单位为min。

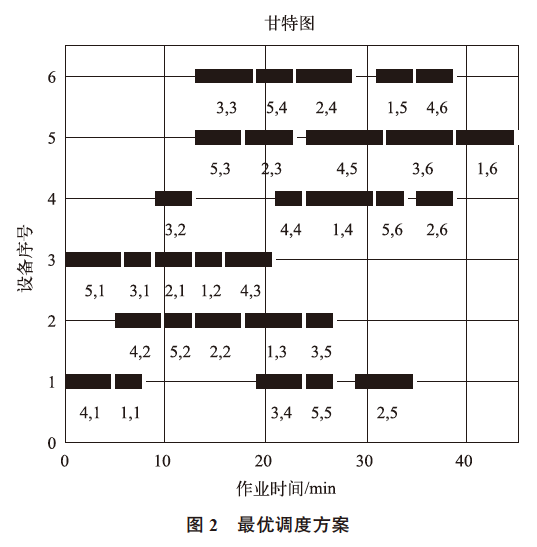
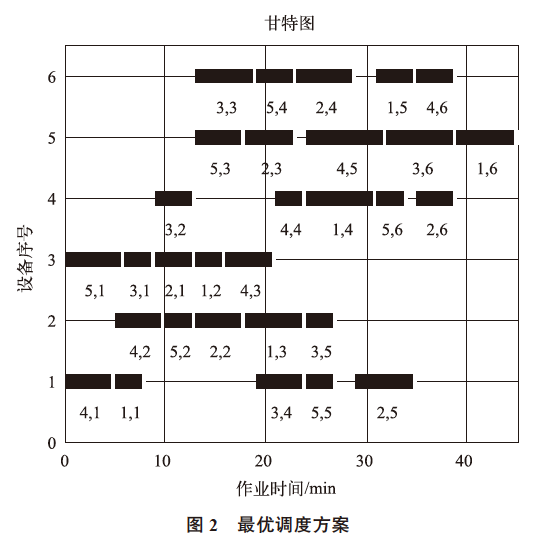
当对一个解进行解码后，根据每个机器上所对应作业工序的先后顺序，确定同一机器上各作业对应工序的先后顺序，再根据每项作业工序之间先后的关系及作业时间，计算出每台机器上进行各项作业相关工序的开始时间和完工时间。仿真结果：得到最优粒子为[4 4 5 3 1 3 2 5 1 2 4 5 3 5 2 3 4 4 5 2 1 1 2 3 5 2 3 1 1 4]，最大完工时间为45min。仿真得到的最优调度方案如图2 所示，图中进度条下方的标注数字，前者表示任务序号，后者表示工序顺序。

采用本文提出的并行模拟退火算法运行1 000 次求解最优粒子，算法平均运行时间为3.43 s；采用传统模拟退火算法运行1 000 次求解最优粒子，算法平均运行时间为25.27 s。通过OpenMP+CUDA 的多任务调度机制，对多个串并行计算任务进行粗粒度的任务分割与调度，提高了任务间的并行率，从而使得模拟退火算法计算效率得到较大提升，使算法在执行数秒后返回一个近似最优解， 即通过基于GPU 的并行模拟退火算法使可实时完成生产调度问题的解算。

结论

生产调度问题在实际生产中具有广泛的应用，是计算机集成制造系统中的一个关键环节。智能调度是制造系统运行优化的核心，通过智能调度能逐渐降低制造企业的生产成本，提升排产效果，提高经济价值。本文在分析模拟退火算法的基础上，将基于GPU 的并行模拟退火算法用于解决生产调度问题。通过仿真试验，实现了不同任务的智能化生产排序，并为每道工序选择最优的加工机器。该算法思路清晰、原理简单，证实了该算法解决生产调度问题的有效性，同时该算法具有较高的运行效率，有望应用于MES 中实时完成生产任务的智能调度。

为确保智能调度算法在实际生产系统中取得更好效果，考虑下一步将重点围绕以下两方面继续开展研究：

1）优化目标函数，目前的研究成果在解决车间调度问题时，所要优化的目标基本都是最大完工时间最小化， 这仅仅是企业关注的一项指标，实际需求还需要考虑到工时偏差、零件报废等问题。因此，未来在对车间调度问题的研究中，可以考虑更倾向于多目标优化。

2）改进模拟退火算法，传统模拟算法由于前期遍历解空间范围有限，导致过早收敛不能得到全局最优解。通过改进Monte-Carlo 准则，使算法具备跳出局部极值能力和避免参数敏感、过早收敛的问题。

3）借助大数据、云计算和物联网技术发展，通过信息化手段将企业ERP 系统、MES、知识管理及IT 资源等整合互联，实现数据信息和计算能力的共享，更好地适应企业多业务融合、协同高效的智能调度需求。

（文章来源：智能制造IMS）